Lexical Analysis: The source code is broken down into a stream of tokens, where each token represents a basic element of the source code such as a keyword, identifier, operator, or punctuation symbol.
Syntax Analysis (Parsing): The tokens generated in the lexical analysis phase are then parsed to ensure they form a valid syntax tree, which represents the structure of the source code according to the programming language grammar.
Semantic Analysis: This phase checks for semantic errors, such as type mismatches and undefined variables, and builds a symbol table, which contains information about the variables, functions, and their attributes used in the source code.
Intermediate Code Generation: The compiler generates an intermediate code, such as three-address code, which is easier for the compiler to work with than the source code.
Code Optimization: The intermediate code is optimized to improve its efficiency, for example, by removing redundant operations and reordering instructions to take advantage of processor pipelining.
Code Generation: The final phase generates the machine code from the optimized intermediate code, which can then be executed by the computer's hardware.
These phases are interrelated, and the output of one phase is used as input to the next. The phases are executed in a specific order, and each phase builds on the output of the previous phase to produce the final machine code.
Specification and recognition of token explain
In computer science and programming, a token is a basic unit of syntax that represents a meaningful piece of information. Tokens can include keywords, identifiers, operators, literals, and symbols that are used to form valid expressions, statements, and other constructs in a programming language.
Token recognition is the process of identifying these tokens from a stream of characters or source code. This is typically done by a program called a lexer, which reads the source code and generates a stream of tokens that can be used by a parser to analyze the code's structure and meaning.
Token specification, on the other hand, involves defining the rules for what characters and sequences of characters should be recognized as valid tokens in a particular programming language or application. This is typically done using regular expressions or other pattern-matching techniques to specify the syntax and structure of the language.
Overall, token recognition and specification are important parts of the process of parsing and executing programming code, and are fundamental to the functioning of programming languages and compilers.
What is statement
In computer programming, a statement is a complete instruction or command that performs a specific action, often within a larger block of code.
A statement can include one or more expressions, which are combinations of values, operators, and functions that perform a specific operation. For example, in the following code snippet, the "if" statement is used to test a condition, and the "print" statement is used to output a message to the user:
Example python
x = 5
if x > 3:
print("x is greater than 3")
Other types of statements in programming languages can include loops, which allow a block of code to be repeated multiple times, and function calls, which execute a specific set of code with a given set of arguments.
Statements are a fundamental building block of programming, and are used to control the flow of execution, modify data, and interact with external systems and resources
Following questions and answers are image based remember page numbers
Q1. LL(1) Parsing Algorithm
LL(1) is a type of parsing algorithm used in compiler design. It stands for "left-to-right, leftmost derivation, with 1 look-ahead symbol".In LL(1) parsing, the input string is read from left to right, and the parsing algorithm attempts to construct a leftmost derivation of the input string. At each step, the parser looks at the current input symbol and the next input symbol (the "look-ahead" symbol) to decide which production rule to apply. The parser uses a parsing table that maps a combination of the current input symbol and the look-ahead symbol to the appropriate production rule.The LL(1) parsing algorithm has some advantages over other parsing algorithms, such as its simplicity and efficiency. However, it also has some limitations. For example, LL(1) parsers cannot handle all types of grammars, particularly those that are left-recursive or ambiguous. To handle such grammars, more powerful parsing algorithms such as LR parsers are used.

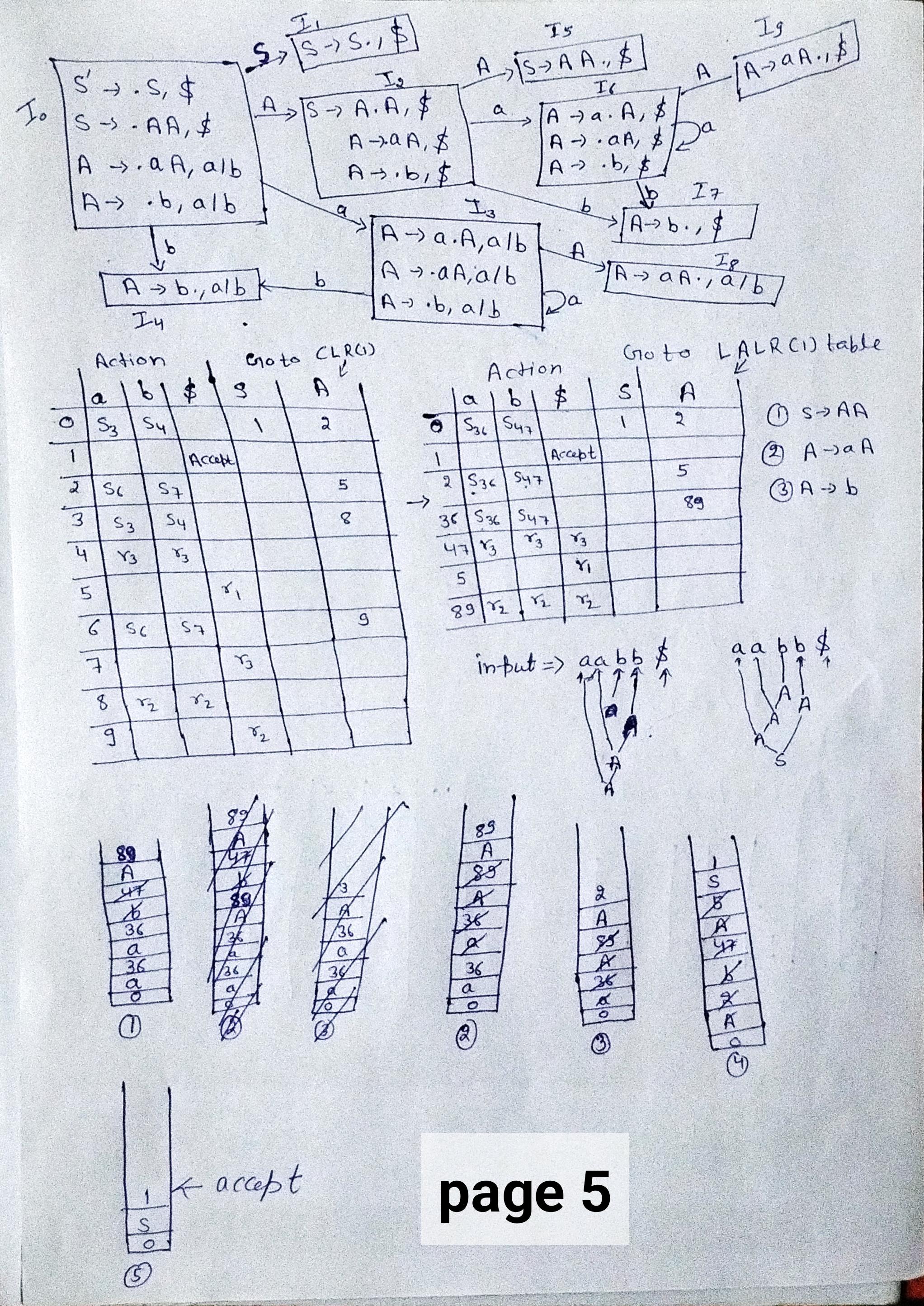
Q4. CLR(1) is a parsing algorithm used in compiler design. It stands for "Canonical LR with 1 look-ahead symbol".
In CLR(1) parsing, the input string is read from left to right, and the parsing algorithm attempts to construct a bottom-up parse tree of the input string. The parser uses a state machine (the LR(0) automaton) to keep track of the current state of the parse and a set of parsing tables (the CLR(1) parsing tables) to determine which action to take at each step.
The CLR(1) parsing tables contain entries for each possible combination of state and look-ahead symbol, and the entries specify the action to take (shift, reduce, or accept) and the state to transition to. The algorithm uses these tables to make parsing decisions based on the current state and the next input symbol.
CLR(1) parsing is more powerful than LL(1) parsing because it can handle more types of grammars, including left-recursive and ambiguous grammars. However, CLR(1) parsing can be more complex and computationally expensive than LL(1) parsing because it requires constructing the LR(0) automaton and the CLR(1) parsing tables.
In summary, CLR(1) is a parsing algorithm used in compiler design that constructs a bottom-up parse tree of an input string by reading the input from left to right and using a state machine and parsing tables to determine which action to take at each step based on the current state and the next input symbol (the look-ahead symbol). CLR(1) parsing is more powerful than LL(1) parsing but can be more complex and computationally expensive.
Q2.LR(0) is a parsing algorithm used in compiler design. It stands for "Left-to-right, Rightmost derivation with 0 look-ahead symbol".In LR(0) parsing, the input string is read from left to right and a parse tree is constructed using a stack-based approach. The algorithm uses a state machine called the LR(0) automaton to keep track of the current state of the parse. At each step, the parser looks at the current input symbol and the top symbol on the stack to determine which action to take.The LR(0) automaton has states that represent the current parsing context, which is defined as the portion of the input string that has been parsed so far and the set of symbols that can appear immediately after it. The automaton transitions between states based on the next input symbol and the top symbol on the stack.LR(0) parsing is a bottom-up parsing technique, meaning it constructs the parse tree from the bottom up by reducing symbols to their corresponding nonterminals. LR(0) parsing is powerful enough to handle a wide range of grammars, including those that are left-recursive and ambiguous.However, LR(0) parsing can still have limitations when dealing with some grammars that have conflicts, such as shift-reduce and reduce-reduce conflicts. To handle these conflicts, more advanced parsing algorithms, such as LR(1), LALR(1), and CLR(1), were developed.In summary, LR(0) is a bottom-up parsing algorithm used in compiler design that constructs a parse tree by reading the input string from left to right and using a state machine (LR(0) automaton) to determine the parsing context and which action to take based on the current input symbol and the top symbol on the stack. LR(0) parsing can handle a wide range of grammars but may still have conflicts that need to be resolved by more advanced parsing algorithms.Q5.LALR(1) is a parsing algorithm used in compiler design. It stands for "Look-Ahead LR with 1 item".
In LALR(1) parsing, the input string is read from left to right, and the parsing algorithm constructs a bottom-up parse tree of the input string. The algorithm uses a state machine called the LALR(1) automaton, which is similar to the LR(0) automaton used in LR(0) parsing but with additional information about the look-ahead symbols.
The LALR(1) automaton has states that represent the current parsing context, which includes the portion of the input string that has been parsed so far and the set of symbols that can appear immediately after it. However, unlike LR(0) parsing, LALR(1) parsing uses a more sophisticated look-ahead mechanism that takes into account more information about the input.
Specifically, LALR(1) parsing considers a set of items that include the LR(0) items from the LR(0) automaton augmented with look-ahead symbols. The look-ahead symbols are used to resolve conflicts that can arise in LR(0) parsing due to the limited look-ahead capability of the LR(0) automaton.
LALR(1) parsing is more powerful than LR(0) parsing because it can handle more types of grammars, including those that are left-recursive and ambiguous. However, LALR(1) parsing is less powerful than CLR(1) parsing because it uses a more limited look-ahead mechanism.
In summary, LALR(1) is a parsing algorithm used in compiler design that constructs a bottom-up parse tree of an input string by reading the input from left to right and using a state machine (LALR(1) automaton) that takes into account more information about the input than the LR(0) automaton. LALR(1) parsing can handle more types of grammars than LR(0) parsing, but fewer than CLR(1) parsing.
Q3.SLR(1) is a parsing algorithm used in compiler design. It stands for "Simple LR with 1 item".
In SLR(1) parsing, the input string is read from left to right, and the parsing algorithm constructs a bottom-up parse tree of the input string. The algorithm uses a state machine called the SLR(1) automaton, which is a simplified version of the LR(0) automaton used in LR(0) parsing.
The SLR(1) automaton has states that represent the current parsing context, which includes the portion of the input string that has been parsed so far and the set of symbols that can appear immediately after it. However, unlike LALR(1) parsing, SLR(1) parsing uses a simpler look-ahead mechanism that considers only the follow set of the non-terminal symbols.
The follow set of a non-terminal symbol is the set of symbols that can follow the non-terminal in a valid parse of the grammar. By using the follow sets, the SLR(1) parser can detect and resolve conflicts that arise due to shift-reduce or reduce-reduce conflicts.
SLR(1) parsing is less powerful than LALR(1) and CLR(1) parsing because it uses a more limited look-ahead mechanism. However, SLR(1) parsing is simpler and easier to implement than LALR(1) and CLR(1) parsing, and it can handle a large class of grammars, including those that are left-recursive and unambiguous.
In summary, SLR(1) is a parsing algorithm used in compiler design that constructs a bottom-up parse tree of an input string by reading the input from left to right and using a state machine (SLR(1) automaton) that uses a simple look-ahead mechanism based on the follow sets of the non-terminal symbols. SLR(1) parsing is less powerful than LALR(1) and CLR(1) parsing but is simpler and can handle a large class of grammars.
Q6.SDD stands for Syntax Directed Definition, which is a formalism used in compiler design to specify the translation of a programming language syntax into machine code or some other target format.
An SDD is a set of rules that associates a set of semantic actions with the production rules of a grammar. Each semantic action specifies some computation that is to be performed when a particular production rule is used during parsing. The computation can involve constructing an abstract syntax tree, generating machine code, or performing some other operation that depends on the syntax of the input program.
The SDD defines a mapping between the input program and its output by specifying the translation of each production rule in the grammar. Each production rule is associated with a set of semantic actions, which can be used to compute the output corresponding to that rule.
SDDs can be used to implement various compiler phases such as lexical analysis, syntax analysis, semantic analysis, and code generation. For example, during syntax analysis, the SDD is used to construct an abstract syntax tree that represents the structure of the input program, and during code generation, the SDD is used to generate machine code that corresponds to the input program.
In summary, SDDs are a formalism used in compiler design to specify the translation of a programming language syntax into machine code or some other target format. They associate a set of semantic actions with the production rules of a grammar, defining a mapping between the input program and its output. SDDs can be used to implement various compiler phases such as lexical analysis, syntax analysis, semantic analysis, and code generation.
Q7.Left recursion is a grammar construction in which a non-terminal symbol can derive a string that begins with itself. For example, consider the following grammar rule:
A → Aα | β
This rule is left-recursive because it allows the non-terminal symbol A to derive a string that begins with itself. This can cause problems in parsing because the parser may go into an infinite loop trying to parse such a grammar rule.
To eliminate left recursion, we can use the following algorithm:
Create a new non-terminal symbol A' that will replace A in the original grammar rule.
Rewrite the original rule as follows:
A → βA'
A' → αA' | ε
where ε denotes the empty string.
The new rule for A' is right-recursive and ensures that all productions of A' derive strings that do not begin with A. The ε production is added to ensure that A' can derive the empty string.
The process can be repeated for any other left-recursive rules in the grammar. By eliminating left recursion, we can ensure that the grammar is suitable for use in parsing algorithms such as LL(1), SLR(1), LALR(1), and CLR(1).
In summary, left recursion is a grammar construction that can cause problems in parsing. To eliminate left recursion, we can create a new non-terminal symbol and rewrite the original rule to ensure that all productions of the new symbol are right-recursive and do not derive strings that begin with the original non-terminal.





Comments
Post a Comment