Computer organisation anaylization (COA) practical file
Practical1
Aim decimal number to binary number
Algorithm step1 start
Step 2 enter value
Step3 While(d!=0) {
B[i] = d%2;I++; D = d/2;
Step4For(i=(i-1); i>=0; i--) Cout<<b[i];
Step 5 stop
#include<iostream>
Using namespace std;
Int main()
{ Int d, b[20], i=0;
Cout<<”Enter
the Decimal Number: “;
Cin>>d;
While(d!=0)
{ B[i] = d%2;
I++; D = d/2;
} Cout<<”\n
Binary Value: “;
For(i=(i-1);
i>=0; i--)
Cout<<b[i]; Return 0;}
Input/output
Aim binary number to decimal number
Algorithm step1 start
Step 2 enter value
Step 3 while(b!=0) { r = b%10;d = d + (r*i); i = i*2;
b=b/10;}
Step4 stop
Code #include<iostream>
Using namespace std;
Int main()
{
Int b, d=0, i=1,
r;
Cout<<”Enter
any Binary Number:“;
Cin>>b;
While(b!=0)
{R = b%10; D = d + (r*i); I = i*2;
B = b/10;}
Cout<<”\n Decimal Value = “<<d; Return 0;}
Input/output
Practical 2 |
Aim-> 1’s compliment decimal number to binary number
Code-> #include<iostream>
Using namespace std;
Void onescomp(int num){
Int rem;
If (num <= 1) {
Cout << !num;
Return; }
Rem = num % 2;
Onescomp(num / 2);
Cout << !rem;}
Int main(){
Int dec;
Cout <<
“Enter the number : “;
Cin >> dec;
If (dec < 0)
Cout << dec
<< “ is not a positive integer.” << endl;
Else { Cout
<< “The ones complement form of “ << dec << “ is “;
Onescomp(dec);
Cout << endl;
}
Return 0;}
Algorithm->step1 start
Step 2Int rem;
If (num <= 1) {
Cout << !num;
Return; }Rem = num % 2;
Onescomp(num / 2);
Cout << !rem;}
Input and output
Practical 3
Aim-> 2’s compliment of decimal number to binary number
Algorithm step1 start
Step2 for(i=3; i>=0; i--) {
x=n&(1<<i);
if(x==0)
cout<<"0";
else
cout<<"1"; }
n=~n;
n=n+1;
Step3 stop
Code #include <iostream>
using namespace std;
int main()
{ int n,i,x;
cout<<"
Please, Enter a Number : ";
cin>>n;
cout<<"\n The binary equivalent of the number : \n ";
for(i=3; i>=0;
i--)
{
x=n&(1<<i);
if(x==0)
cout<<"0";
else
cout<<"1"; }
n=~n;
n=n+1;
cout<<"\n
The 2's complement of the number :\n "
for(i=3; i>=0;
i--)
{ x=n&(1<<i);
if(x==0)
cout<<"0";
else
cout<<"1";
}
return 0;}
Input/output
| Practical 4
Aim simulation of AND,OR and NOT gate A) AND gate- Theory->The AND gate is so named because, if 0 is called “false” and 1 is called “true,” the gate acts in the same way as the logical “and” operator. The following illustration and table show the circuit symbol and logic combinations for an AND gate. (In the symbol, the input terminals are at left and the output terminal is at right.) The output is “true” when both inputs are “true.” Otherwise, the output is “false.” In other words, the output is 1 only when both inputs one AND two are 1. |
B)OR gate
The OR gate gets its name from the fact that it behaves after the fashion of the logical inclusive “or.” The output is “true” if either or both of the inputs are “true.” If both inputs are “false,” then the output is “false.” In other words, for the output to be 1, at least input one OR two must be 1.
C)NOT gate->
A logical inverter, sometimes called a NOT gate to
differentiate it from other types of electronic inverter devices, has only one
input. It reverses the logic state. If the input is 1, then the output is 0. If
the input is 0, then the output is 1.
| Practical 5 |
Aim->simulation gate of XOR and XNOR gate
A)XOR gate->
The XOR ( exclusive-OR ) gate acts in the same way as the
logical “either/or.” The output is “true” if either, but not both, of the
inputs are “true.” The output is “false” if both inputs are “false” or if both
inputs are “true.” Another way of looking at this circuit is to observe that
the output is 1 if the inputs are different, but 0 if the inputs are the same.
B)XNOR gate->
The XNOR (exclusive-NOR) gate is a combination XOR gate
followed by an inverter. Its output is “true” if the inputs are the same, and
“false” if the inputs are different.
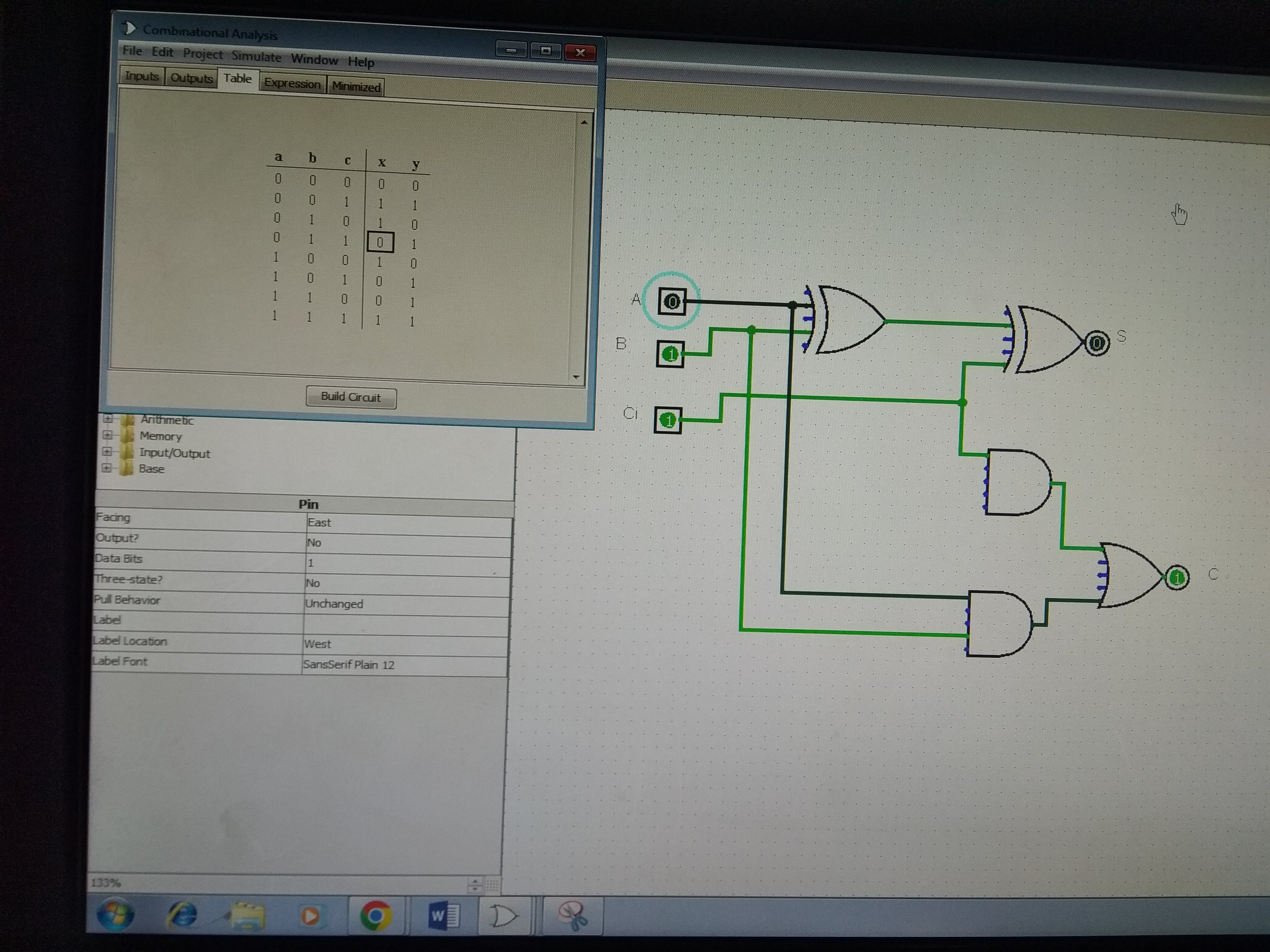
Aim->simulation of half adder and full adder
A)half adder->A
half adder is a type of adder, an electronic circuit that performs the addition
of numbers. The half adder is able to add two single binary digits and provide
the output plus a carry value. It has two inputs, called A and B, and two
outputs S (sum) and C (carry).
B)
Full adder->
the
full adder was developed. The full adder is used to add three 1-bit binary
numbers A, B, and carry C. The full adder has three input states and two output
states i.e., sum and carry.
| Practical 7 |
Aim simulation of ripple carry
adder and look ahead carry adder
A)
Ripple carry adder->
each carry bit gets rippled into the next stage. In a ripple carry adder the sum and carry out bits of any half adder stage is not valid until the carry in of that stage occurs.
| B)Look ahead carry adder-> |
reduces the propagation delay by introducing
more complex hardware.
| Practical 8 |
Aim-> simulation of half
substruction and full substruction
A) Half substructor->This circuit is used to subtract two single bit binary numbers A and B. The 'diff' and 'borrow' are two output states of the half subtractor.
| B)Full substructor-> |
The
full subtractor is used to subtract three 1-bit numbers A, B, and C, which are
minuend, subtrahend, and borrow, respectively. The full subtractor has three
input states and two output states i.e., diff and borrow.
| Practical 9 |
Aim-> simulation of
multiplexer and demultiplexer
A)
Multiplexer->
The binary information is
received from the input lines and directed to the output line. On the basis of
the values of the selection lines, one of these data inputs will be connected
to the output.
| B)Demultiplexer-> |
A
De-multiplexer is a combinational circuit that has only 1 input line and 2N output
lines. De-multiplexer is opposite to the multiplexer.
| Practical 10 |
Aim->simulation of encoder and
decoder
A)
Encoder->
The
combinational circuits that change the binary information into N output lines
are known as Encoders. The binary information is passed in the form
of 2N input lines. The output lines define the N-bit code for
the binary information.
| B)Decoder-> |
The combinational circuit
that change the binary information into 2N output lines is
known as Decoders. The binary information is passed in the
form of N input lines. The output lines define the 2N-bit code for
the binary information. In simple words, the Decoder performs the reverse operation of the Encoder. At a time, only one input line is activated for simplicity.
The produced 2N-bit output code is equivalent to the binary
information.


















Comments
Post a Comment